来自今天的算法作业

动态规划——最长公共子序列

最长公共子序列（LCS）是一个在一个序列集合中（通常为两个序列）用来查找所有序列中最长子序列的问题（子序列不需要在原序列中占用连续的位置）。

• 动态规划方程

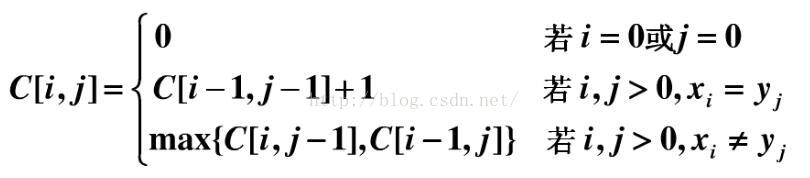
• 查填表过程

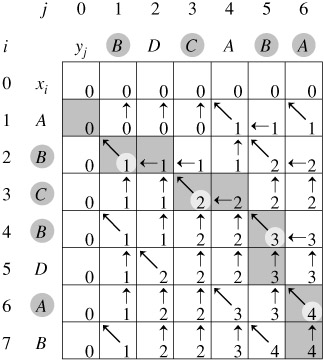
• 代码

#include <bits/stdc++.h>
using namespace std;
void LCS(int i,int j,char *str1,int **b){
	if(i==0||j==0)
		return ;
	if(b[i][j]==1){
		LCS(i-1,j-1,str1,b);
		cout<<str1[i-1];		//c中的第i行元素对应str1的第i-1个元素
	}	
	else if(b[i][j]==2){
		LCS(i-1,j,str1,b);
	}
	else
		LCS(i,j-1,str1,b);
}
int main()
{
	char str1[101],str2[101];
	int c[101][101],i,j;
	cout<<"请输入第一个字符串："<<endl;
	gets(str1);
	cout<<"请输入第二个字符串："<<endl;
	gets(str2);
	int n=strlen(str1);
	int m=strlen(str2);
	int **b=new int*[n+1];  
    for(i=0;i<=n;i++)  
        b[i]=new int[m+1]; 
	for(i=0;i<=n;i++)	//将表中第0列初始化为0 
		c[i][0]=0;
	for(j=0;j<=m;j++)	//将表中第0行初始化为0	
		c[0][j]=0;	 
	for(i=1;i<=n;i++){
		for(j=1;j<=m;j++){
			if(str1[i-1]==str2[j-1]){
				c[i][j]=c[i-1][j-1]+1;
				b[i][j]=1;
			}
			else if(c[i-1][j]>=c[i][j-1]){
				c[i][j]=c[i-1][j];
				b[i][j]=2;
			}
			else{
				c[i][j]=c[i][j-1];
				b[i][j]=3;
			}
		}
	}	
	cout<<"最长公共子序列长度为："<<c[n][m]<<endl;
	cout<<"此子序列为：";
	LCS(n,m,str1,b); 
	return 0;	
} 

• 总结

此次的作业中有一个小地方弄了很久。就是c[][]这个二维数组的0行0列都是直接置0的，从c[][]数组第1行第1列的开始才是有用的，而str1和str2两个字符串数组都是从0开始的，那么c数组第i行的元素其实对应的是str的i-1个元素。所以在写的时候有两处：输出子序列时和判断两个序列元素相等时都要注意！

此算法的时间复杂度为O（nm）